what happens to the wavelength of a wave when the frequency decreases?

Spatial flow of the moving ridge—the distance over which the wave'southward shape repeats, and thus the changed of the spatial frequency

The wavelength of a sine wave, λ, can exist measured between any 2 points with the aforementioned stage, such as between crests (on top), or troughs (on bottom), or respective cypher crossings equally shown.

In physics, the wavelength is the spatial period of a periodic wave—the altitude over which the moving ridge's shape repeats.^{[one] [2]} It is the altitude between sequent corresponding points of the same phase on the wave, such as 2 side by side crests, troughs, or zero crossings, and is a characteristic of both traveling waves and continuing waves, as well every bit other spatial moving ridge patterns.^{[iii] [four]} The changed of the wavelength is called the spatial frequency. Wavelength is unremarkably designated by the Greek letter lambda (λ). The term wavelength is also sometimes applied to modulated waves, and to the sinusoidal envelopes of modulated waves or waves formed by interference of several sinusoids.^[5]

Assuming a sinusoidal moving ridge moving at a stock-still wave speed, wavelength is inversely proportional to frequency of the wave: waves with higher frequencies have shorter wavelengths, and lower frequencies have longer wavelengths.^[6]

Wavelength depends on the medium (for example, vacuum, air, or water) that a wave travels through. Examples of waves are audio waves, light, water waves and periodic electrical signals in a conductor. A audio wave is a variation in air pressure level, while in light and other electromagnetic radiations the strength of the electric and the magnetic field vary. Water waves are variations in the height of a body of water. In a crystal lattice vibration, atomic positions vary.

The range of wavelengths or frequencies for wave phenomena is chosen a spectrum. The proper name originated with the visible calorie-free spectrum but now can be applied to the unabridged electromagnetic spectrum as well as to a audio spectrum or vibration spectrum.

Sinusoidal waves [edit]

In linear media, any moving ridge pattern can be described in terms of the contained propagation of sinusoidal components. The wavelength λ of a sinusoidal waveform traveling at abiding speed ${\displaystyle v}$ is given by^[7]

${\displaystyle \lambda ={\frac {v}{f}}\,\,,}$

where ${\displaystyle v}$ is called the phase speed (magnitude of the stage velocity) of the wave and ${\displaystyle f}$ is the moving ridge's frequency. In a dispersive medium, the stage speed itself depends upon the frequency of the moving ridge, making the relationship between wavelength and frequency nonlinear.

In the example of electromagnetic radiation—such as light—in free space, the phase speed is the speed of light, about 3×ten⁸ m/south. Thus the wavelength of a 100 MHz electromagnetic (radio) wave is about: iii×ten⁸ yard/south divided past 10⁸ Hz = iii metres. The wavelength of visible light ranges from deep ruby, roughly 700 nm, to violet, roughly 400 nm (for other examples, come across electromagnetic spectrum).

For sound waves in air, the speed of sound is 343 m/south (at room temperature and atmospheric pressure). The wavelengths of audio frequencies audible to the human ear (20 Hz–20 kHz) are thus between approximately 17 m and 17 mm, respectively. Somewhat higher frequencies are used by bats and so they can resolve targets smaller than 17 mm. Wavelengths in audible sound are much longer than those in visible calorie-free.

Sinusoidal standing waves in a box that constrains the stop points to be nodes will have an integer number of half wavelengths fitting in the box.

A continuing wave (blackness) depicted as the sum of two propagating waves traveling in reverse directions (ruddy and blue)

Standing waves [edit]

A continuing wave is an undulatory movement that stays in one place. A sinusoidal continuing wave includes stationary points of no motion, called nodes, and the wavelength is twice the altitude between nodes.

The upper figure shows three continuing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary weather condition) determining which wavelengths are immune. For case, for an electromagnetic wave, if the box has ideal metal walls, the condition for nodes at the walls results because the metal walls cannot support a tangential electric field, forcing the wave to have zero amplitude at the wall.

The stationary wave tin be viewed as the sum of ii traveling sinusoidal waves of oppositely directed velocities.^[8] Consequently, wavelength, period, and wave velocity are related just every bit for a traveling wave. For example, the speed of light can be determined from observation of standing waves in a metal box containing an platonic vacuum.

Mathematical representation [edit]

Traveling sinusoidal waves are oft represented mathematically in terms of their velocity v (in the x direction), frequency f and wavelength λ as:

${\displaystyle y(10,\ t)=A\cos \left(2\pi \left({\frac {x}{\lambda }}-ft\right)\right)=A\cos \left({\frac {2\pi }{\lambda }}(x-vt)\right)}$

where y is the value of the moving ridge at any position x and time t, and A is the amplitude of the wave. They are also commonly expressed in terms of wavenumber k (2π times the reciprocal of wavelength) and athwart frequency ω (2π times the frequency) as:

${\displaystyle y(x,\ t)=A\cos \left(kx-\omega t\right)=A\cos \left(g(10-vt)\right)}$

in which wavelength and wavenumber are related to velocity and frequency as:

${\displaystyle k={\frac {2\pi }{\lambda }}={\frac {2\pi f}{v}}={\frac {\omega }{5}},}$

or

${\displaystyle \lambda ={\frac {ii\pi }{yard}}={\frac {2\pi v}{\omega }}={\frac {5}{f}}.}$

In the second course given above, the phase (kx − ωt) is often generalized to (one thousand•r − ωt), past replacing the wavenumber g with a wave vector that specifies the direction and wavenumber of a plane wave in 3-space, parameterized past position vector r. In that case, the wavenumber thousand, the magnitude of k, is still in the same relationship with wavelength as shown above, with five being interpreted as scalar speed in the direction of the wave vector. The start class, using reciprocal wavelength in the phase, does not generalize equally easily to a wave in an capricious direction.

Generalizations to sinusoids of other phases, and to complex exponentials, are too common; see plane moving ridge. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real function of the complex exponential in the wave

${\displaystyle Ae^{i\left(kx-\omega t\right)}.}$

General media [edit]

Wavelength is decreased in a medium with slower propagation.

Refraction: upon entering a medium where its speed is lower, the wave changes management.

Separation of colors past a prism (click for animation)

The speed of a wave depends upon the medium in which information technology propagates. In item, the speed of light in a medium is less than in vacuum, which ways that the same frequency will stand for to a shorter wavelength in the medium than in vacuum, as shown in the figure at correct.

This change in speed upon inbound a medium causes refraction, or a modify in direction of waves that encounter the interface between media at an angle.^[nine] For electromagnetic waves, this change in the angle of propagation is governed past Snell's law.

The wave velocity in one medium not only may differ from that in another, but the velocity typically varies with wavelength. Every bit a result, the change in direction upon entering a unlike medium changes with the wavelength of the wave.

For electromagnetic waves the speed in a medium is governed by its refractive index co-ordinate to

${\displaystyle v={\frac {c}{north(\lambda _{0})}},}$

where c is the speed of low-cal in vacuum and due north(λ₀) is the refractive index of the medium at wavelength λ₀, where the latter is measured in vacuum rather than in the medium. The corresponding wavelength in the medium is

${\displaystyle \lambda ={\frac {\lambda _{0}}{n(\lambda _{0})}}.}$

When wavelengths of electromagnetic radiation are quoted, the wavelength in vacuum commonly is intended unless the wavelength is specifically identified equally the wavelength in some other medium. In acoustics, where a medium is essential for the waves to exist, the wavelength value is given for a specified medium.

The variation in speed of light with wavelength is known equally dispersion, and is too responsible for the familiar miracle in which calorie-free is separated into component colors by a prism. Separation occurs when the refractive alphabetize inside the prism varies with wavelength, and then dissimilar wavelengths propagate at different speeds inside the prism, causing them to refract at unlike angles. The mathematical relationship that describes how the speed of light within a medium varies with wavelength is known every bit a dispersion relation.

Nonuniform media [edit]

Diverse local wavelengths on a crest-to-crest footing in an bounding main moving ridge approaching shore^[10]

Wavelength can be a useful concept fifty-fifty if the wave is non periodic in space. For example, in an ocean wave approaching shore, shown in the figure, the incoming wave undulates with a varying local wavelength that depends in part on the depth of the sea floor compared to the wave height. The assay of the wave tin can be based upon comparison of the local wavelength with the local water depth.^[x]

A sinusoidal wave travelling in a nonuniform medium, with loss

Waves that are sinusoidal in time simply propagate through a medium whose properties vary with position (an inhomogeneous medium) may propagate at a velocity that varies with position, and as a result may not be sinusoidal in infinite. The figure at right shows an case. As the wave slows down, the wavelength gets shorter and the aamplitude increases; after a place of maximum response, the short wavelength is associated with a high loss and the moving ridge dies out.

The analysis of differential equations of such systems is oftentimes done approximately, using the WKB method (likewise known every bit the Liouville–Green method). The method integrates phase through infinite using a local wavenumber, which can exist interpreted as indicating a "local wavelength" of the solution equally a function of fourth dimension and space.^{[11] [12]} This method treats the arrangement locally as if it were compatible with the local properties; in item, the local wave velocity associated with a frequency is the only matter needed to estimate the corresponding local wavenumber or wavelength. In add-on, the method computes a slowly changing amplitude to satisfy other constraints of the equations or of the physical system, such as for conservation of energy in the wave.

Crystals [edit]

A wave on a line of atoms can exist interpreted according to a variety of wavelengths.

Waves in crystalline solids are not continuous, considering they are equanimous of vibrations of detached particles arranged in a regular lattice. This produces aliasing because the same vibration can be considered to have a variety of different wavelengths, as shown in the figure.^[xiii] Descriptions using more than than ane of these wavelengths are redundant; it is conventional to choose the longest wavelength that fits the phenomenon. The range of wavelengths sufficient to provide a description of all possible waves in a crystalline medium corresponds to the moving ridge vectors bars to the Brillouin zone.^[xiv]

This indeterminacy in wavelength in solids is of import in the assay of wave phenomena such as energy bands and lattice vibrations. It is mathematically equivalent to the aliasing of a point that is sampled at discrete intervals.

More general waveforms [edit]

Near-periodic waves over shallow h2o

The concept of wavelength is most frequently applied to sinusoidal, or about sinusoidal, waves, because in a linear system the sinusoid is the unique shape that propagates with no shape change – just a phase change and potentially an aamplitude change.^[15] The wavelength (or alternatively wavenumber or moving ridge vector) is a characterization of the wave in space, that is functionally related to its frequency, every bit constrained by the physics of the system. Sinusoids are the simplest traveling wave solutions, and more circuitous solutions tin exist built up by superposition.

In the special case of dispersion-free and uniform media, waves other than sinusoids propagate with unchanging shape and constant velocity. In certain circumstances, waves of unchanging shape likewise tin can occur in nonlinear media; for example, the effigy shows ocean waves in shallow water that accept sharper crests and flatter troughs than those of a sinusoid, typical of a cnoidal wave,^[16] a traveling wave so named because it is described by the Jacobi elliptic part of yard-th lodge, usually denoted as cn(x; thousand).^[17] Large-amplitude ocean waves with sure shapes can propagate unchanged, because of properties of the nonlinear surface-moving ridge medium.^[18]

Wavelength of a periodic but not-sinusoidal waveform.

If a traveling wave has a fixed shape that repeats in space or in time, information technology is a periodic moving ridge.^[19] Such waves are sometimes regarded every bit having a wavelength even though they are not sinusoidal.^[20] As shown in the figure, wavelength is measured betwixt sequent respective points on the waveform.

Moving ridge packets [edit]

A propagating wave package

Localized wave packets, "bursts" of moving ridge action where each moving ridge packet travels as a unit, find awarding in many fields of physics. A wave packet has an envelope that describes the overall amplitude of the wave; inside the envelope, the distance between adjacent peaks or troughs is sometimes called a local wavelength.^{[21] [22]} An instance is shown in the figure. In general, the envelope of the wave packet moves at a speed different from the constituent waves.^[23]

Using Fourier assay, moving ridge packets tin be analyzed into space sums (or integrals) of sinusoidal waves of different wavenumbers or wavelengths.^[24]

Louis de Broglie postulated that all particles with a specific value of momentum p have a wavelength λ = h/p, where h is Planck'south constant. This hypothesis was at the basis of quantum mechanics. Nowadays, this wavelength is chosen the de Broglie wavelength. For example, the electrons in a CRT display have a De Broglie wavelength of nearly 10⁻¹³ m. To prevent the wave function for such a particle being spread over all space, de Broglie proposed using wave packets to represent particles that are localized in space.^[25] The spatial spread of the wave bundle, and the spread of the wavenumbers of sinusoids that brand upwards the packet, represent to the uncertainties in the particle'due south position and momentum, the product of which is divisional by Heisenberg uncertainty principle.^[24]

Interference and diffraction [edit]

Double-slit interference [edit]

Pattern of light intensity on a screen for light passing through two slits. The labels on the right refer to the difference of the path lengths from the ii slits, which are idealized hither equally point sources.

When sinusoidal waveforms add, they may reinforce each other (constructive interference) or abolish each other (destructive interference) depending upon their relative stage. This miracle is used in the interferometer. A simple example is an experiment due to Young where light is passed through two slits.^[26] As shown in the figure, calorie-free is passed through two slits and shines on a screen. The path of the lite to a position on the screen is different for the 2 slits, and depends upon the angle θ the path makes with the screen. If we suppose the screen is far enough from the slits (that is, due south is large compared to the slit separation d) and then the paths are nearly parallel, and the path divergence is just d sin θ. Accordingly, the condition for effective interference is:^[27]

${\displaystyle d\sin \theta =m\lambda \ ,}$

where chiliad is an integer, and for destructive interference is:

${\displaystyle d\sin \theta =(m+1/2)\lambda \ .}$

Thus, if the wavelength of the light is known, the slit separation can be determined from the interference pattern or fringes, and vice versa.

For multiple slits, the pattern is ^[28]

${\displaystyle I_{q}=I_{1}\sin ^{2}\left({\frac {q\pi m\sin \alpha }{\lambda }}\right)/\sin ^{2}\left({\frac {\pi g\sin \alpha }{\lambda }}\right)\ ,}$

where q is the number of slits, and m is the grating constant. The beginning factor, I ₁, is the single-slit consequence, which modulates the more than speedily varying 2nd cistron that depends upon the number of slits and their spacing. In the figure I ₁ has been set to unity, a very rough approximation.

The issue of interference is to redistribute the light, so the energy contained in the light is not altered, just where it shows up.^[29]

Single-slit diffraction [edit]

Diffraction blueprint of a double slit has a unmarried-slit envelope.

The notion of path difference and constructive or subversive interference used above for the double-slit experiment applies too to the display of a unmarried slit of calorie-free intercepted on a screen. The main result of this interference is to spread out the light from the narrow slit into a broader image on the screen. This distribution of wave energy is chosen diffraction.

Ii types of diffraction are distinguished, depending upon the separation between the source and the screen: Fraunhofer diffraction or far-field diffraction at large separations and Fresnel diffraction or near-field diffraction at close separations.

In the assay of the single slit, the non-nothing width of the slit is taken into business relationship, and each indicate in the aperture is taken as the source of 1 contribution to the beam of light (Huygens' wavelets). On the screen, the calorie-free arriving from each position inside the slit has a different path length, albeit maybe a very small difference. Consequently, interference occurs.

In the Fraunhofer diffraction blueprint sufficiently far from a single slit, within a small-bending approximation, the intensity spread South is related to position ten via a squared sinc part:^[30]

${\displaystyle S(u)=\mathrm {sinc} ^{2}(u)=\left({\frac {\sin \pi u}{\pi u}}\right)^{2}\ ;}$ with ${\displaystyle u={\frac {xl}{\lambda R}}\ ,}$

where Fifty is the slit width, R is the distance of the pattern (on the screen) from the slit, and λ is the wavelength of calorie-free used. The function Southward has zeros where u is a not-zilch integer, where are at x values at a separation proportion to wavelength.

Diffraction-express resolution [edit]

Diffraction is the fundamental limitation on the resolving power of optical instruments, such as telescopes (including radiotelescopes) and microscopes.^[31] For a round discontinuity, the diffraction-express epitome spot is known every bit an Blusterous deejay; the distance ten in the single-slit diffraction formula is replaced by radial altitude r and the sine is replaced by 2J ₁, where J _i is a first order Bessel function.^[32]

The resolvable spatial size of objects viewed through a microscope is limited according to the Rayleigh criterion, the radius to the start null of the Airy disk, to a size proportional to the wavelength of the light used, and depending on the numerical aperture:^[33]

${\displaystyle r_{Airy}=1.22{\frac {\lambda }{2\mathrm {NA} }}\ ,}$

where the numerical aperture is defined equally ${\displaystyle \mathrm {NA} =n\sin \theta \;}$ for θ beingness the one-half-bending of the cone of rays accepted by the microscope objective.

The angular size of the central bright portion (radius to first null of the Airy disk) of the image diffracted by a circular discontinuity, a mensurate most commonly used for telescopes and cameras, is:^[34]

${\displaystyle \delta =1.22{\frac {\lambda }{D}}\ ,}$

where λ is the wavelength of the waves that are focused for imaging, D the entrance student bore of the imaging organisation, in the same units, and the angular resolution δ is in radians.

As with other diffraction patterns, the pattern scales in proportion to wavelength, then shorter wavelengths tin can lead to college resolution.

Subwavelength [edit]

The term subwavelength is used to describe an object having ane or more dimensions smaller than the length of the wave with which the object interacts. For instance, the term subwavelength-diameter optical fibre means an optical fibre whose diameter is less than the wavelength of low-cal propagating through information technology.

A subwavelength particle is a particle smaller than the wavelength of lite with which it interacts (see Rayleigh scattering). Subwavelength apertures are holes smaller than the wavelength of calorie-free propagating through them. Such structures have applications in extraordinary optical transmission, and zilch-mode waveguides, among other areas of photonics.

Subwavelength may also refer to a phenomenon involving subwavelength objects; for example, subwavelength imaging.

Angular wavelength [edit]

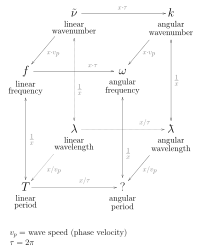
Relationship between wavelength, angular wavelength, and other wave properties.

A quantity related to the wavelength is the angular wavelength (as well known equally reduced wavelength), unremarkably symbolized past ƛ (lambda-bar). Information technology is equal to the "regular" wavelength "reduced" past a gene of 2π (ƛ = λ/2π). It is usually encountered in quantum mechanics, where information technology is used in combination with the reduced Planck constant (symbol ħ, h-bar) and the angular frequency (symbol ω) or angular wavenumber (symbol chiliad).

Come across also [edit]

• Emission spectrum
• Envelope (waves)
• Fraunhofer lines – dark lines in the solar spectrum, traditionally used as standard optical wavelength references
• Index of moving ridge articles
• Length measurement
• Spectral line
• Spectroscopy
• Spectrum

References [edit]

1. ^ Hecht, Eugene (1987). Eyes (2nd ed.). Addison Wesley. pp. 15–16. ISBN0-201-11609-X.
2. ^ Brian Hilton Flowers (2000). "§21.two Periodic functions". An introduction to numerical methods in C++ (2nd ed.). Cambridge University Press. p. 473. ISBN0-19-850693-vii.
3. ^ Raymond A. Serway; John W. Jewett (2006). Principles of physics (4th ed.). Cengage Learning. pp. 404, 440. ISBN0-534-49143-X.
4. ^ A. A. Sonin (1995). The surface physics of liquid crystals. Taylor & Francis. p. 17. ISBN2-88124-995-7.
5. ^ Keqian Zhang & Dejie Li (2007). Electromagnetic Theory for Microwaves and Optoelectronics. Springer. p. 533. ISBN978-iii-540-74295-one.
6. ^ Theo Koupelis & Karl F. Kuhn (2007). In Quest of the Universe . Jones & Bartlett Publishers. p. 102. ISBN978-0-7637-4387-1. wavelength lambda light sound frequency wave speed.
7. ^ David C. Cassidy; Gerald James Holton; Floyd James Rutherford (2002). Understanding physics. Birkhäuser. pp. 339 ff. ISBN0-387-98756-viii.
8. ^ John Avison (1999). The World of Physics. Nelson Thornes. p. 460. ISBN978-0-17-438733-vi.
9. ^ To aid imagination, this bending of the wave frequently is compared to the analogy of a column of marching soldiers crossing from solid footing into mud. See, for instance, Raymond T. Pierrehumbert (2010). Principles of Planetary Climate. Cambridge Academy Printing. p. 327. ISBN978-0-521-86556-2.
10. ^ ^{a b} Paul R Pinet (2009). op. cit. p. 242. ISBN978-0-7637-5993-3.
11. ^ Bishwanath Chakraborty (2007). Principles of Plasma Mechanics. New Historic period International. p. 454. ISBN978-81-224-1446-2.
12. ^ Jeffrey A. Hogan & Joseph D. Lakey (2005). Time-frequency and fourth dimension-scale methods: adaptive decompositions, uncertainty principles, and sampling. Birkhäuser. p. 348. ISBN978-0-8176-4276-i.
13. ^ Meet Figure 4.20 in A. Putnis (1992). Introduction to mineral sciences . Cambridge University Printing. p. 97. ISBN0-521-42947-i. and Figure 2.iii in Martin T. Dove (1993). Introduction to lattice dynamics (4th ed.). Cambridge Academy Printing. p. 22. ISBN0-521-39293-iv.
14. ^ Manijeh Razeghi (2006). Fundamentals of solid state applied science (2d ed.). Birkhäuser. pp. 165 ff. ISBN0-387-28152-5.
15. ^ Encounter Lord Rayleigh (1890). "Wave theory". Encyclopædia Britannica (9th ed.). The Henry Chiliad Allen Company. p. 422.
16. ^ Valery Due north. Pilipchuk (2010). "Figure 4.iv: Transition from quasi-harmonic to cnoidal wave". Nonlinear Dynamics: Between Linear and Bear upon Limits. Springer. p. 127. ISBN978-3642127984.
17. ^ Andrei Ludu (2012). "§eighteen.3 Special functions". Nonlinear Waves and Solitons on Contours and Closed Surfaces (2d ed.). Springer. pp. 469 ff. ISBN978-3642228940.
18. ^ Alfred Osborne (2010). "Chapter ane: Brief history and overview of nonlinear water waves". Nonlinear Ocean Waves and the Inverse Scattering Transform. Academic Press. pp. 3 ff. ISBN978-0-12-528629-9.
19. ^ Alexander McPherson (2009). "Waves and their backdrop". Introduction to Macromolecular Crystallography (ii ed.). Wiley. p. 77. ISBN978-0-470-18590-2.
20. ^ Eric Stade (2011). Fourier Analysis. John Wiley & Sons. p. one. ISBN978-1-118-16551-5.
21. ^ Peter R. The netherlands (1995). The Quantum Theory of Motion: An Account of the de Broglie–Bohm Causal Interpretation of Quantum Mechanics. Cambridge University Press. p. 160. ISBN978-0-521-48543-2.
22. ^ Jeffery Cooper (1998). Introduction to partial differential equations with MATLAB. Springer. p. 272. ISBN0-8176-3967-5. The local wavelength λ of a dispersing moving ridge is twice the distance between two successive zeros. ... the local wavelength and the local wave number one thousand are related past k = 2π / λ.
23. ^ A. T. Fromhold (1991). "Wave bundle solutions". Quantum Mechanics for Applied Physics and Engineering (Reprint of Academic Press 1981 ed.). Courier Dover Publications. pp. 59 ff. ISBN0-486-66741-3. (p. 61) ... the private waves move more than slowly than the packet and therefore laissez passer back through the packet as it advances
24. ^ ^{a b} See, for example, Figs. 2.8–2.x in Joy Manners (2000). "Heisenberg'south uncertainty principle". Quantum Physics: An Introduction. CRC Press. pp. 53–56. ISBN978-0-7503-0720-eight.
25. ^ Ming Chiang Li (1980). "Electron Interference". In Fifty. Marton; Claire Marton (eds.). Advances in Electronics and Electron Physics. Vol. 53. Bookish Printing. p. 271. ISBN0-12-014653-3.
26. ^ Greenfield Sluder & David E. Wolf (2007). "Four. Young'south Experiment: Two-Slit Interference". Digital microscopy (third ed.). Academic Press. p. 15. ISBN978-0-12-374025-0.
27. ^ Halliday, Resnick, Walker (2008). "§35-4 Young'south interference experiment". Fundamentals of Physics (Extended 8th ed.). Wiley-India. p. 965. ISBN978-81-265-1442-7. {{cite book}}: CS1 maint: multiple names: authors list (link)
28. ^ Kordt Griepenkerl (2002). "§9.viii.ii Diffraction by a grating". In John West Harris; Walter Benenson; Horst Stöcker; Holger Lutz (eds.). Handbook of physics. Springer. pp. 307 ff. ISBN0-387-95269-ane.
29. ^ Douglas B. Murphy (2002). Fundamentals of calorie-free microscopy and electronic imaging. Wiley/IEEE. p. 64. ISBN0-471-23429-X.
30. ^ John C. Stover (1995). Optical scattering: measurement and analysis (2nd ed.). SPIE Printing. p. 64. ISBN978-0-8194-1934-vii.
31. ^ Graham Saxby (2002). "Diffraction limitation". The science of imaging. CRC Press. p. 57. ISBN0-7503-0734-10.
32. ^ Grant R. Fowles (1989). Introduction to Modern Eyes. Courier Dover Publications. pp. 117–120. ISBN978-0-486-65957-2.
33. ^ James B. Pawley (1995). Handbook of biological confocal microscopy (second ed.). Springer. p. 112. ISBN978-0-306-44826-3.
34. ^ Ray N. Wilson (2004). Reflecting Telescope Optics I: Bones Blueprint Theory and Its Historical Development. Springer. p. 302. ISBN978-3-540-40106-3.

External links [edit]

Wikimedia Commons has media related to Wavelength.

• Conversion: Wavelength to Frequency and vice versa – Sound waves and radio waves
• Educational activity resources for 14–16 years on sound including wavelength
• The visible electromagnetic spectrum displayed in web colors with according wavelengths

buffingtonacessays.blogspot.com

Source: https://en.wikipedia.org/wiki/Wavelength

Share this post